Adaptive control of a novel nonlinear double convection chaotic system

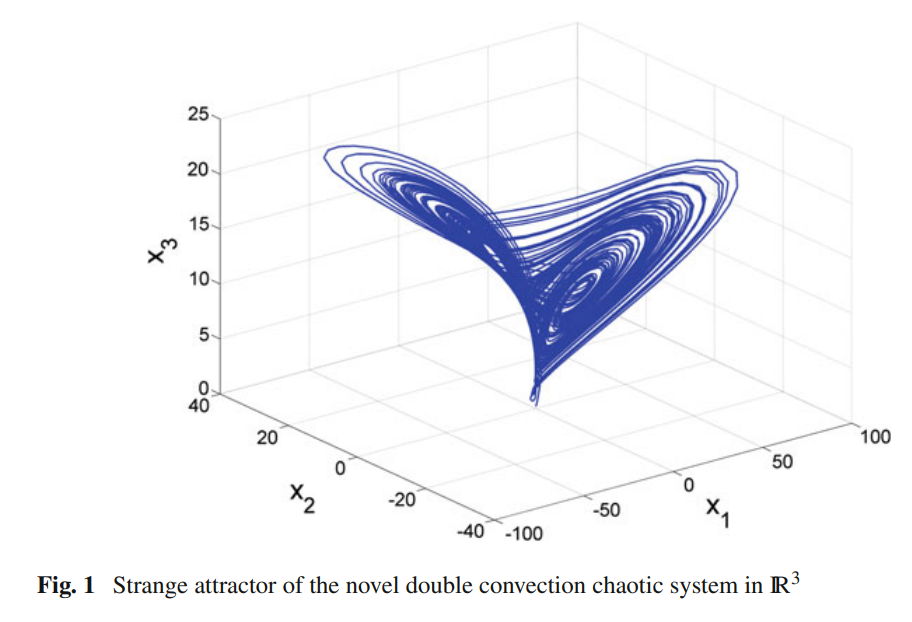
This researchwork describes a six-term novel nonlinear double convection chaotic system with two nonlinearities. First, this work presents the 3-D dynamics of the novel nonlinear double convection chaotic system and depicts the phase portraits of the system. Our novel nonlinear double convection chaotic system is obtained by modifying the dynamics of the Rucklidge chaotic system (1992). Next, the qualitative properties of the novel chaotic system are discussed in detail. The novel chaotic system has three equilibrium points. We show that the equilibrium point at the origin is a saddle point, while the other two equilibrium points are saddle-foci. The Lyapunov exponents of the novel nonlinear double convection chaotic system are obtained as L1 = 0.2089, L2 = 0 and L3 = −3.2123. The Lyapunov dimension of the novel chaotic system is obtained as DL = 2.0650. Next, we present the design of adaptive feedback controller for globally stabilizing the trajectories of the novel nonlinear double convection chaotic system with unknown parameters. Furthermore, we present the design of adaptive feedback controller for achieving complete synchronization of the identical novel nonlinear double convection chaotic systems with unknown parameters. The main adaptive control results are proved using Lyapunov stability theory. MATLAB simulations are depicted to illustrate all the main results derived in this research work for the novel nonlinear double convection system. © Springer International Publishing AG 2017.