Breadcrumb

Generalized Formula for Generating N-Scroll Chaotic Attractors
The generation of Multi-scroll chaotic attractors and chaos theory has gained much attention due to its many usages in a wide range of applications such as image-encryption and random number generators. There have been many previous attempts to establish a system that is able to generate large numbers of n - scroll chaotic attractors by modifying existing systems such as Lorenz and Chua's systems. In this paper, a proposed system based on generalizing Chua's system that has shown its ability to produce an unprecedentedly large number of even and odd chaotic scrolls is introduced. MATLAB
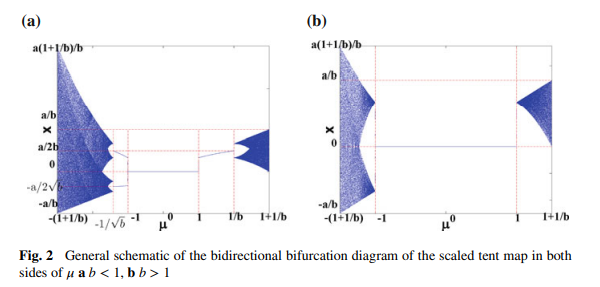
Chaos and bifurcation in controllable jerk-based self-excited attractors
In the recent decades, utilization of chaotic systems has flourished in various engineering applications. Hence, there is an increasing demand on generalized, modified and novel chaotic systems. This chapter combines the general equation of jerk-based chaotic systems with simple scaled discrete chaotic maps. Two continuous chaotic systems based on jerk-equation and discrete maps with scaling parameters are presented. The first system employs the scaled tent map, while the other employs the scaled logistic map. The effects of different parameters on the type of the response of each system are
Self-excited attractors in jerk systems: Overview and numerical investigation of chaos production
Chaos theory has attracted the interest of the scientific community because of its broad range of applications, such as in secure communications, cryptography or modeling multi-disciplinary phenomena. Continuous flows, which are expressed in terms of ordinary differential equations, can have numerous types of post transient solutions. Reporting when these systems of differential equations exhibit chaos represents a rich research field. A self-excited chaotic attractor can be detected through a numerical method in which a trajectory starting from a point on the unstable manifold in the
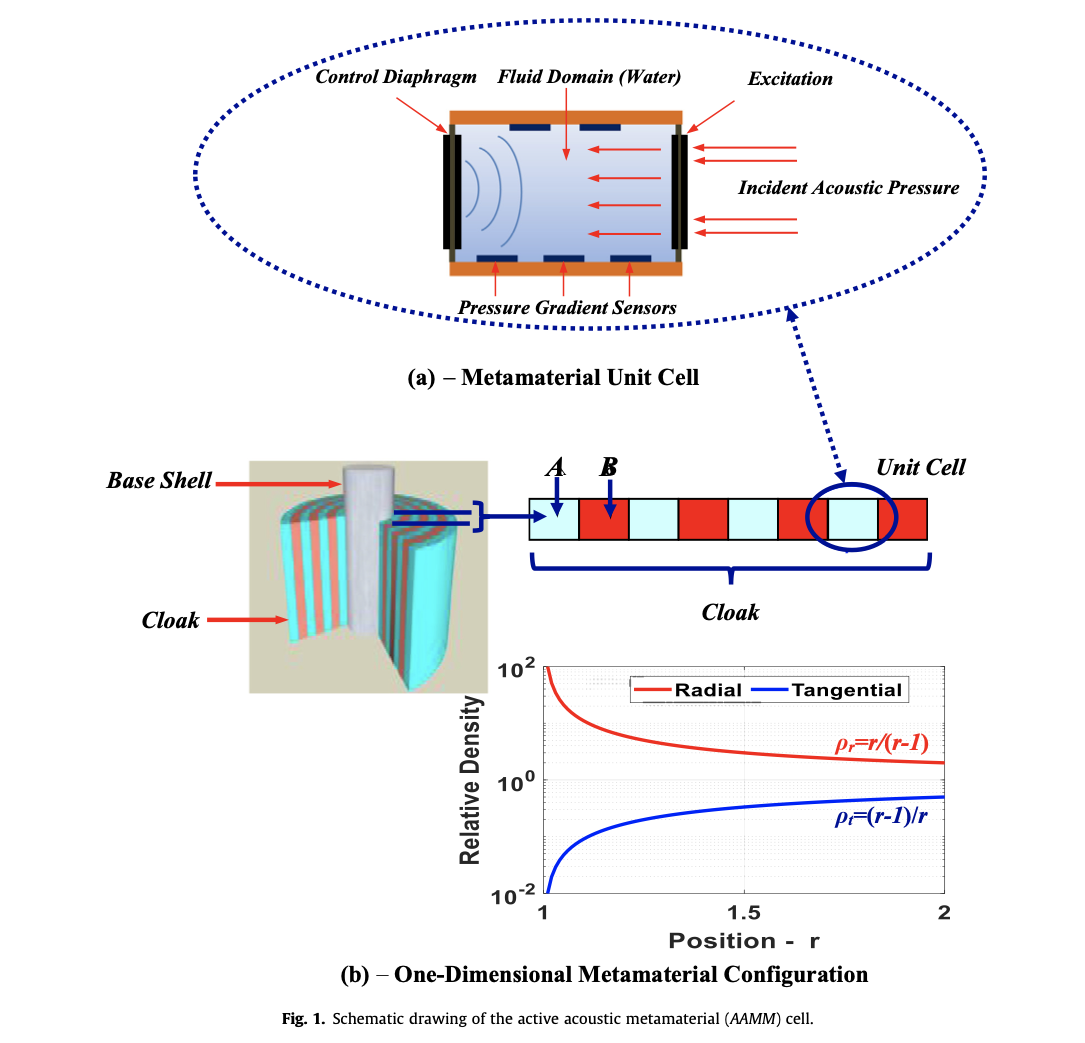
Active control of the dynamic density of acoustic metamaterials
All attempts to develop acoustic metamaterials with prescribed characteristics are based on utilizing the concepts of resonance frequencies of the metamaterial cell structure or on the spatial arrangement of two-or multi-phase domains to realize density or bulk modulus values on the micro scale that influence the wave propagation on the macro scale. In here, a radically different concept is presented whereby active acoustic metamaterial cell has been developed to manipulate the incompressible material dynamic density and reach relative stable values of 0.35–13 times the original fluid domain
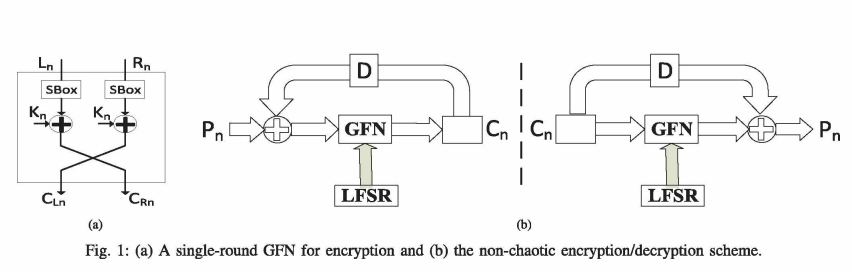
Security and Efficiency of Feistel Networks Versus Discrete Chaos for Lightweight Speech Encryption
This paper compares examples of non-chaotic and chaotic ciphers from the viewpoint of their suitability for speech encryption, especially in real-time and lightweight cipher systems. The non-chaotic encryption scheme depends on a modified Generalized Feistel Network (GFN), Linear Feedback Shift Register (LFSR) and Substitution Boxes (S-Boxes). The chaotic encryption scheme utilizes a generalized modified tent map with multiple modes of operation. The security and efficiency of both schemes are analyzed using the perceptual tests: time waveform and spectrogram; the statistical tests: histogram
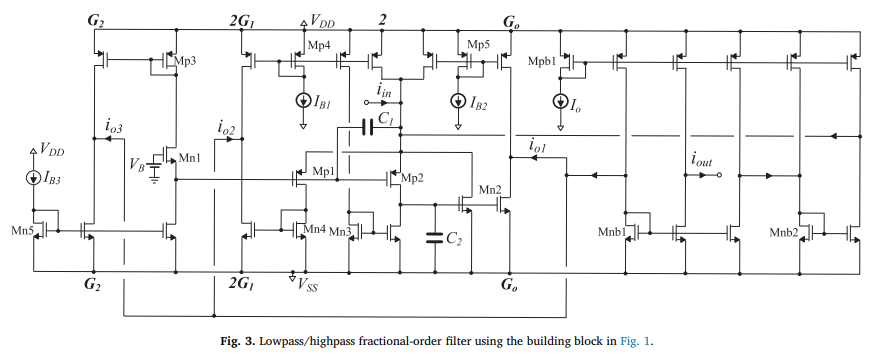
Design and application examples of CMOS fractional-order differentiators and integrators
Reduced complexity CMOS fractional-order differentiator and integrator building blocks are introduced in this work, based on 2 nd -order integer-order transfer function approximations. These blocks are then used for implementing fractional-order filters as well as a Leaky-Integrate-and-Fire Mihalas-Niebur neuron model. Cascading 1 st and 2 nd -order blocks to obtain 5 th -order integer-order transfer functions, improved bandwidth of approximation accuracy is achieved. Furthermore, the realization of fractional-order capacitor and inductor emulators is demonstrated. © 2018 Elsevier Ltd
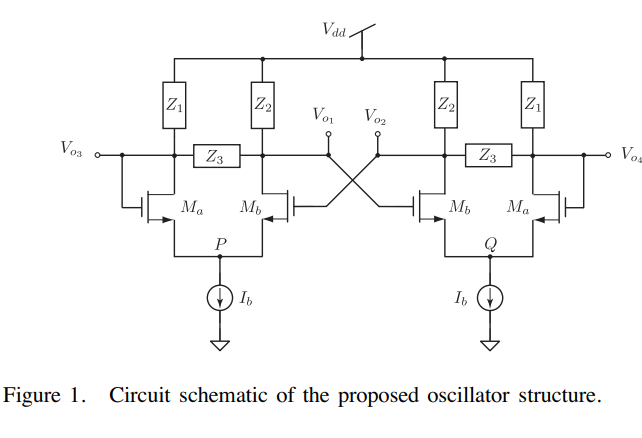
On a class of quadrature phase oscillators using differential pairs
A new class of quadrature phase oscillators based on cross-coupled differential pairs is introduced. This class contains eight possible circuits which produce four output voltages with phase differences of ±π or ±π/2, depending on the choice of output node, and does not require balanced differential-pair loads. Phase error analysis is provided along with experimental and simulation results using discrete MOS and BJT transistors as a proof of concept. © 2018 IEEE
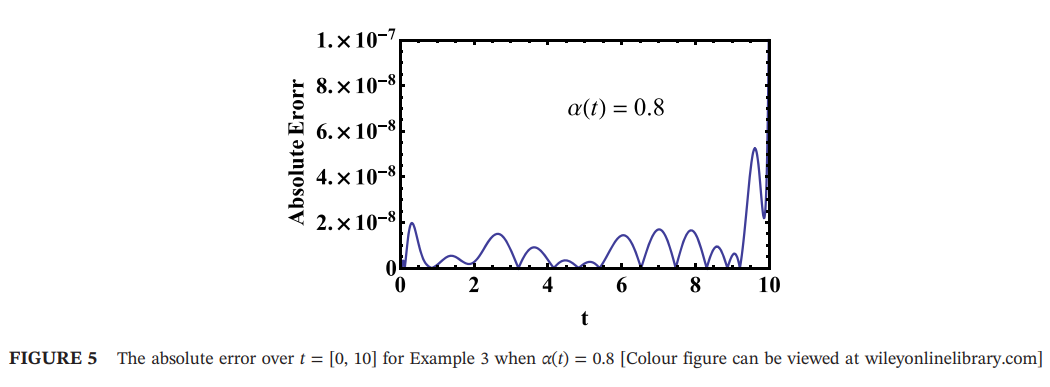
The minimax approach for a class of variable order fractional differential equation
This paper introduces an approximate solution for Liouville-Caputo variable order fractional differential equations with order 0

On the modeling of dispersive transient photocurrent response of organic solar cells
The current methods used for estimating the electrical parameters of organic solar cells (OSC) from time-domain measurements are based on integer-order impedance models. Meanwhile, in the frequency-domain, the adopted circuit models usually contain a constant phase element which is known to capture effectively the fractional-order dispersive behavior of these devices. Therefore, inconsistency arises between the two analyses. In this work, we derive the time-domain relaxation response of an OSC, found to follow a Mittag-Leffler function, using the same fractional-order impedance model. The
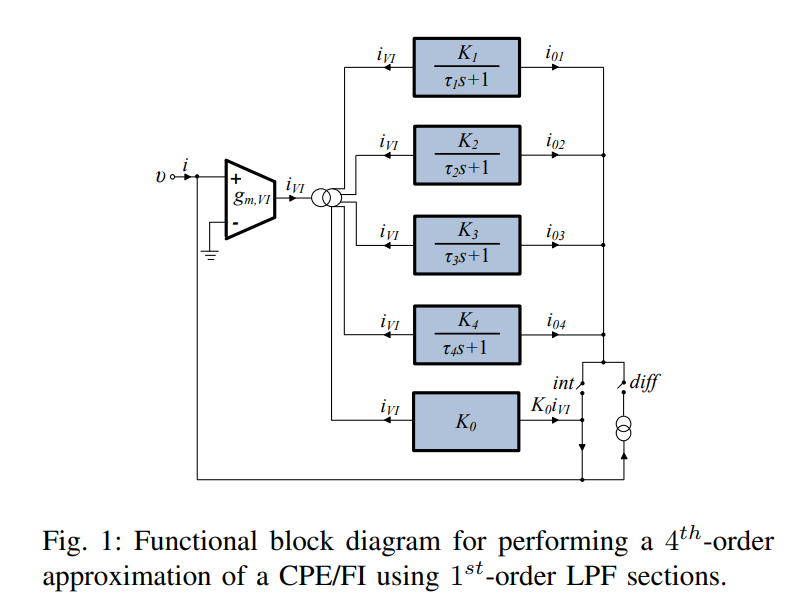
Log-domain implementation of fractional-order element emulators
Novel fractional-order capacitor and inductor em-ulators are presented in this work, which offer fully electronic tunability of their characteristics and, simultaneously, reduced circuit complexity compared to those already introduced in the literature. This has been achieved through the utilization of the log-domain filtering for implementing the approximation of the required fractional-order differentiation/integration stages. The behavior of the presented topology is evaluated using the Cadence software and MOS transistor models provided by the 0.35μm Austria Mikro Systeme CMOS process. ©
Pagination
- Previous page ‹‹
- Page 12
- Next page ››
