Breadcrumb
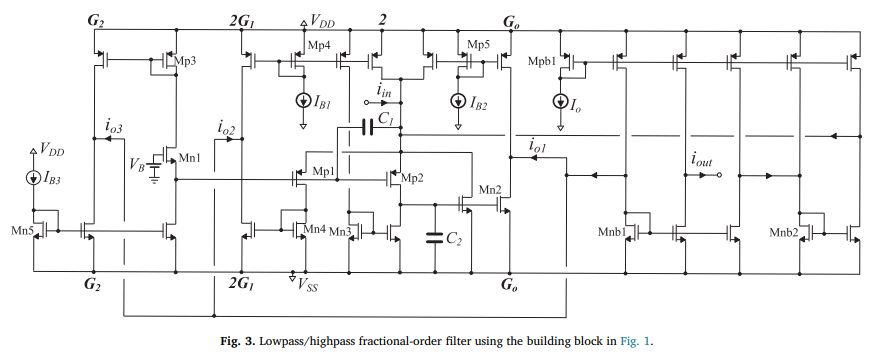
Design and application examples of CMOS fractional-order differentiators and integrators
Reduced complexity CMOS fractional-order differentiator and integrator building blocks are introduced in this work, based on 2 nd -order integer-order transfer function approximations. These blocks are then used for implementing fractional-order filters as well as a Leaky-Integrate-and-Fire Mihalas-Niebur neuron model. Cascading 1 st and 2 nd -order blocks to obtain 5 th -order integer-order transfer functions, improved bandwidth of approximation accuracy is achieved. Furthermore, the realization of fractional-order capacitor and inductor emulators is demonstrated. © 2018 Elsevier Ltd
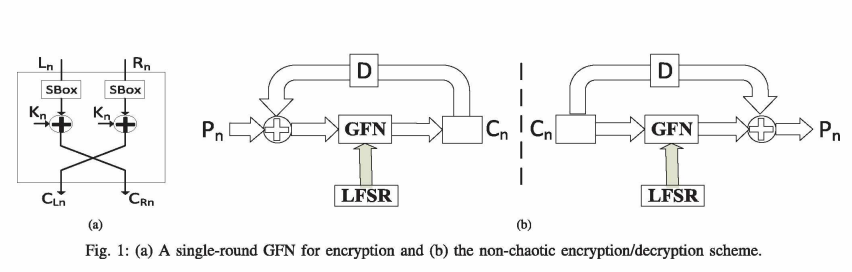
Security and Efficiency of Feistel Networks Versus Discrete Chaos for Lightweight Speech Encryption
This paper compares examples of non-chaotic and chaotic ciphers from the viewpoint of their suitability for speech encryption, especially in real-time and lightweight cipher systems. The non-chaotic encryption scheme depends on a modified Generalized Feistel Network (GFN), Linear Feedback Shift Register (LFSR) and Substitution Boxes (S-Boxes). The chaotic encryption scheme utilizes a generalized modified tent map with multiple modes of operation. The security and efficiency of both schemes are analyzed using the perceptual tests: time waveform and spectrogram; the statistical tests: histogram
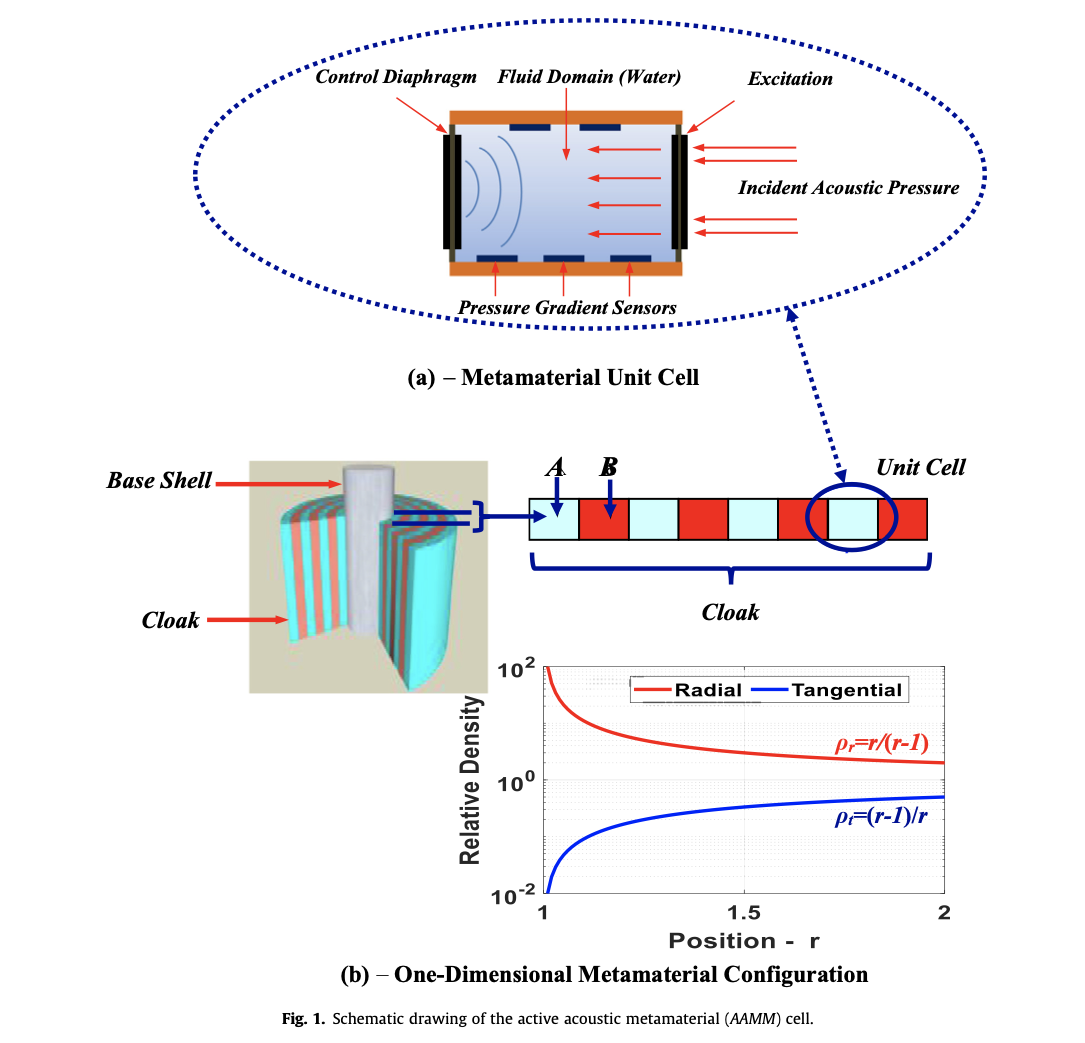
Active control of the dynamic density of acoustic metamaterials
All attempts to develop acoustic metamaterials with prescribed characteristics are based on utilizing the concepts of resonance frequencies of the metamaterial cell structure or on the spatial arrangement of two-or multi-phase domains to realize density or bulk modulus values on the micro scale that influence the wave propagation on the macro scale. In here, a radically different concept is presented whereby active acoustic metamaterial cell has been developed to manipulate the incompressible material dynamic density and reach relative stable values of 0.35–13 times the original fluid domain
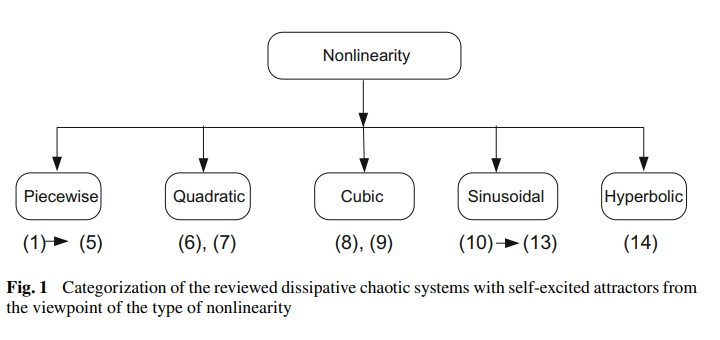
Self-excited attractors in jerk systems: Overview and numerical investigation of chaos production
Chaos theory has attracted the interest of the scientific community because of its broad range of applications, such as in secure communications, cryptography or modeling multi-disciplinary phenomena. Continuous flows, which are expressed in terms of ordinary differential equations, can have numerous types of post transient solutions. Reporting when these systems of differential equations exhibit chaos represents a rich research field. A self-excited chaotic attractor can be detected through a numerical method in which a trajectory starting from a point on the unstable manifold in the
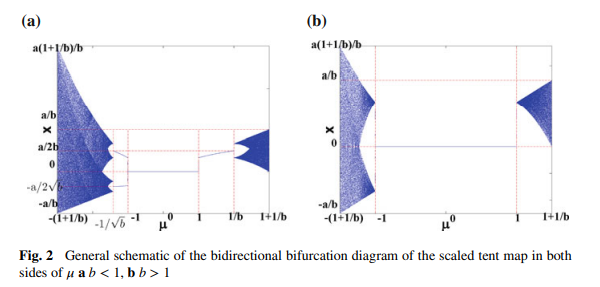
Chaos and bifurcation in controllable jerk-based self-excited attractors
In the recent decades, utilization of chaotic systems has flourished in various engineering applications. Hence, there is an increasing demand on generalized, modified and novel chaotic systems. This chapter combines the general equation of jerk-based chaotic systems with simple scaled discrete chaotic maps. Two continuous chaotic systems based on jerk-equation and discrete maps with scaling parameters are presented. The first system employs the scaled tent map, while the other employs the scaled logistic map. The effects of different parameters on the type of the response of each system are
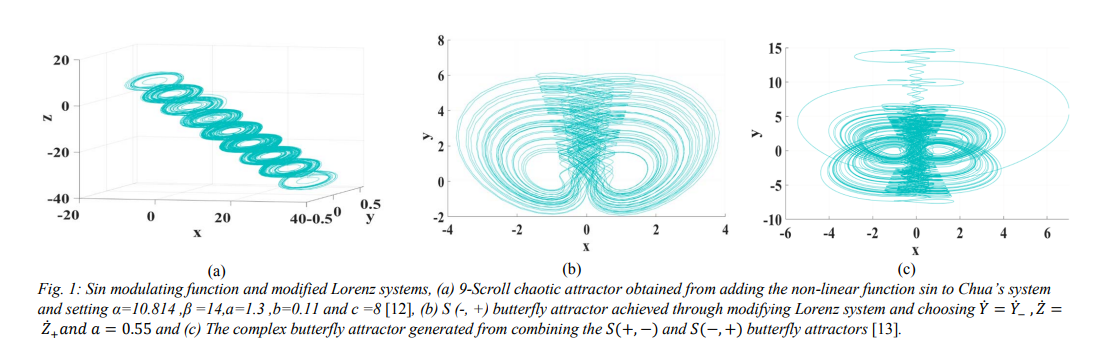
Generalized Formula for Generating N-Scroll Chaotic Attractors
The generation of Multi-scroll chaotic attractors and chaos theory has gained much attention due to its many usages in a wide range of applications such as image-encryption and random number generators. There have been many previous attempts to establish a system that is able to generate large numbers of n - scroll chaotic attractors by modifying existing systems such as Lorenz and Chua's systems. In this paper, a proposed system based on generalizing Chua's system that has shown its ability to produce an unprecedentedly large number of even and odd chaotic scrolls is introduced. MATLAB
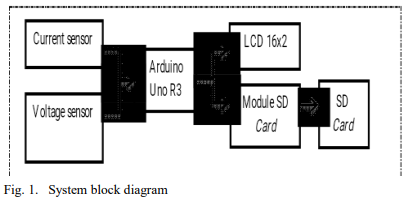
Design and analysis of DC electrical voltage-current data logger device implemented on wind turbine control system
DC electrical voltage-current measuring instrument and data are an instrument used to measure the current and voltage generated by wind turbines and record the measurement results. The function of this instrument is to activate the dummy load on the wind turbine control system to reduce the voltage that exceeds the safe limit when saving electrical energy. The research aimed to manufacture and analyze DC electrical voltage - current measuring instrument using the Arduino Uno based data logger, capable of measuring the DC and voltage generated by Hybrid Power Plants (PLTH) and use the metrology
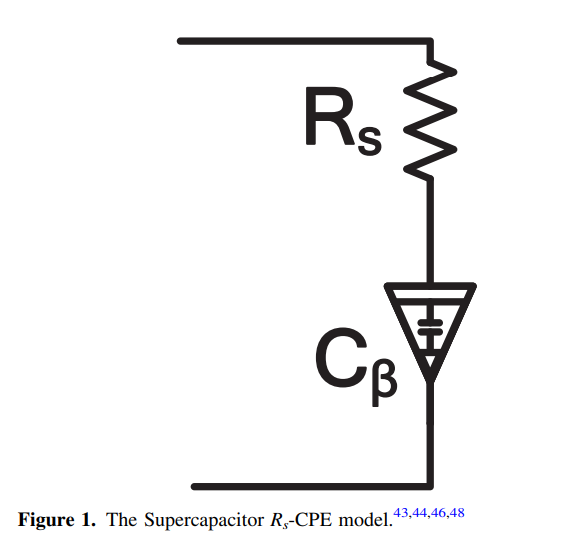
Optimal Charging and Discharging of Supercapacitors
In this paper, we discuss the optimal charging and discharging of supercapacitors to maximize the delivered energy by deploying the fractional and multivariate calculus of variations. We prove mathematically that the constant current is the optimal charging and discharging method under R s -CPE model of supercapacitors. The charging and round-trip efficiencies have been mathematically analyzed for constant current charging and discharging. © 2020 The Electrochemical Society ("ECS"). Published on behalf of ECS by IOP Publishing Limited.
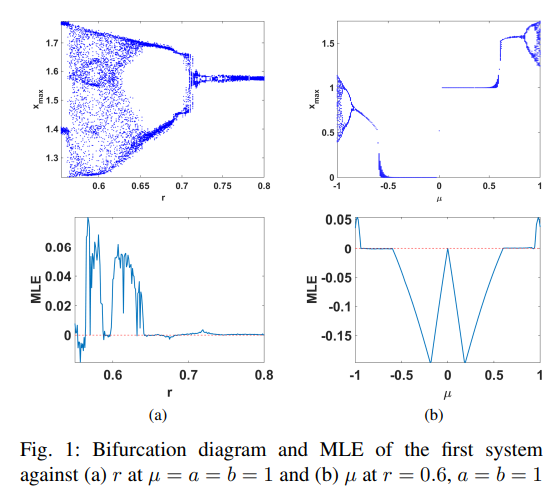
Chaotic systems based on jerk equation and discrete maps with scaling parameters
In the recent decades, applications of chaotic systems have flourished in various fields. Hence, there is an increasing demand on generalized, modified and novel chaotic systems. In this paper, we combine the general equation of jerk-based chaotic systems with simple scaled discrete chaotic maps. Numerical simulations of the properties of two systems, each with four control parameters, are presented. The parameters show interesting behaviors and dependencies among them. In addition, they exhibit controlling capabilities of the ranges of system responses, hence the size of the attractor diagram
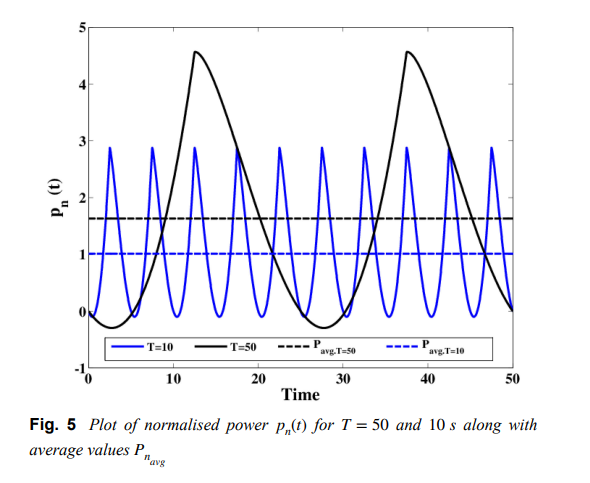
Low-voltage commercial super-capacitor response to periodic linear-with-time current excitation: A case study
The response of a commercial super-capacitor to an applied periodic current excitation in the form of a triangular waveform is investigated in this study. This waveform has a linear-with-time variation which enables linear charging and discharging of the device. A model consisting of a linear resistance Rs and a constant phase element is used to describe the super-capacitor impedance and expressions for the voltage across the device, the power, and stored energy are derived using concepts from fractional calculus. Experimental results are shown and an application of the study to super
Pagination
- Previous page ‹‹
- Page 25
- Next page ››
