Breadcrumb
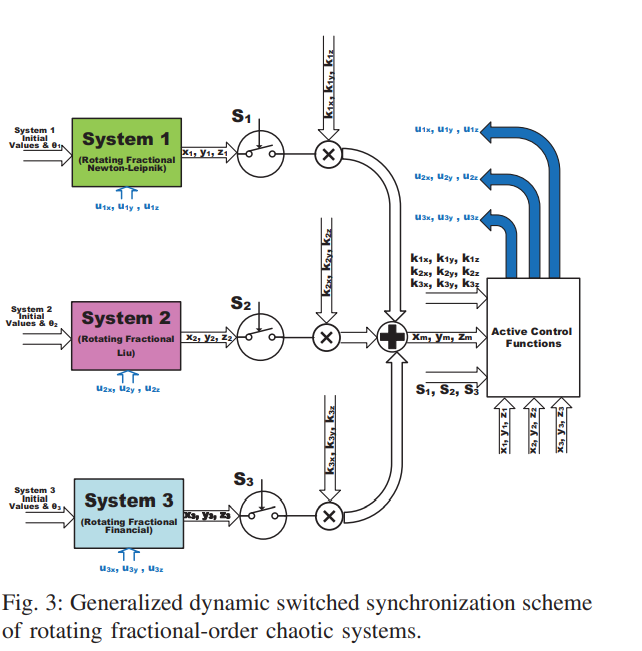
All-Dynamic Synchronization of Rotating Fractional-Order Chaotic Systems
This paper proposes generalized controllable strange attractors through dynamic rotation of fractional-order chaotic systems. Dynamic rotation angle enables the generation of multi-scroll and multi-wing attractors from single and double-scroll ones. The rotating systems are integrated with a generalized dynamic switched synchronization scheme. Dynamic control switches determine whether each system plays the role of master or slave. Based on dynamic scaling factors, the master can be one system or a combination of several ones with new strange attractors. The rotating fractional-order systems
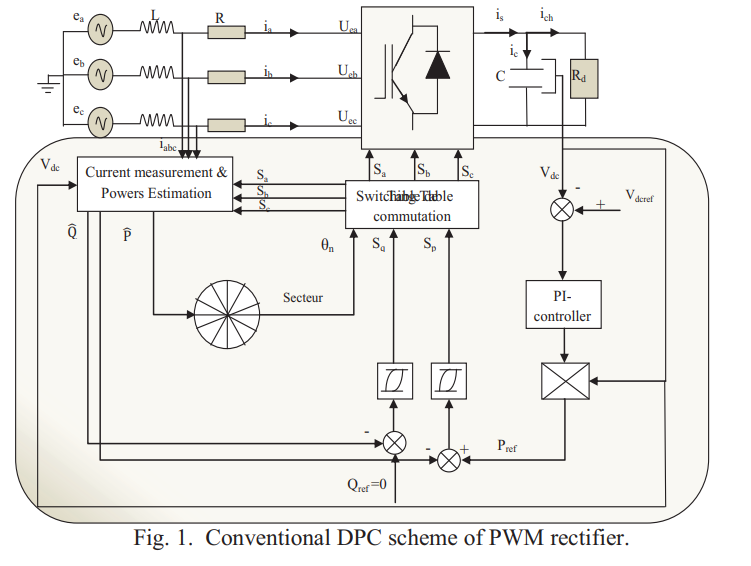
Direct Power Control of a three-phase PWM-Rectifier based on Petri nets for the selection of Switching States
This article proposes a new simple scheme for direct power control of a PWM rectifier without a switch table and voltage sensor. The selection of the switching state of the converter is based on the transition of a Petri net, using the instantaneous active and reactive power tracking errors and the angular position of the network line voltage estimated as variables of Controller input based on Petri nets. Simulation and experimental results demonstrated better performance and verified the validity of the new command with the Petri nets applied to the bridge rectifier connected to the
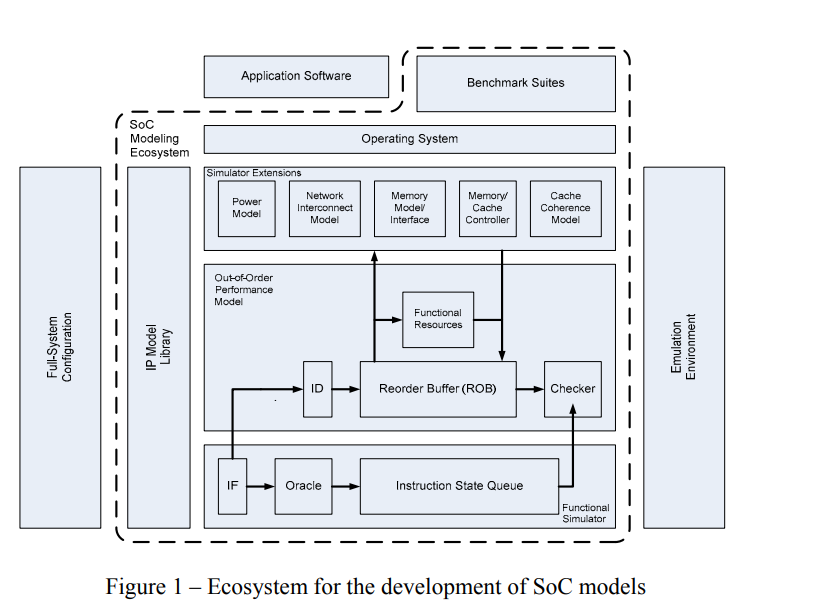
Ecosystems for the development of multi-core and many-core SoC models
Multi-core and many-core Systems-on-Chip (SoC) are growing more complex than ever. Consequently, developing system models for such SoCs to guide and validate architectural and implementation decisions is becoming a daunting task. It consumes a huge amount of time and effort just to get the model up and running. Although these system models can be fairly abstracted, they still require the setup of a complicated platform to model a homogeneous or a heterogeneous mix of processing cores, a network-on-chip, cache memories, input-output interfaces as well as several other functional units. The
Low power clock generator using charge recycling
A major portion of the power consumed in today's systems is due to the clock distribution network. Solutions attempted to reduce clocking power result in low efficiency systems or systems with high complexity control schemes. In this work, a low power clock generator is introduced that can reduce switching power of the clock by almost 75%. This circuit uses the charge recycling concept to achieve such power reduction while utilizing a simple control technique. ©2010 IEEE.
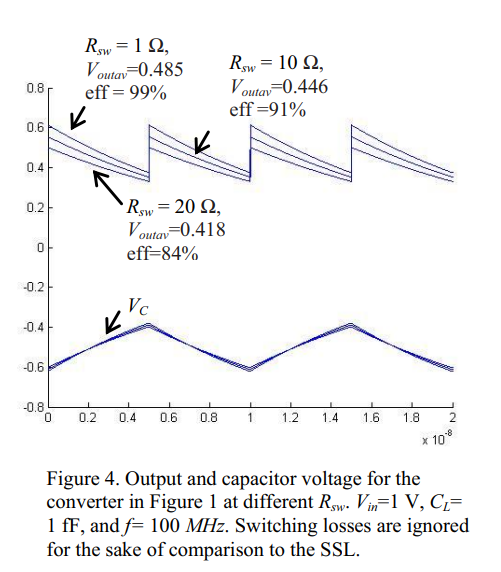
On the accuracy of commonly used loss models in SCVRs
[No abstract available]
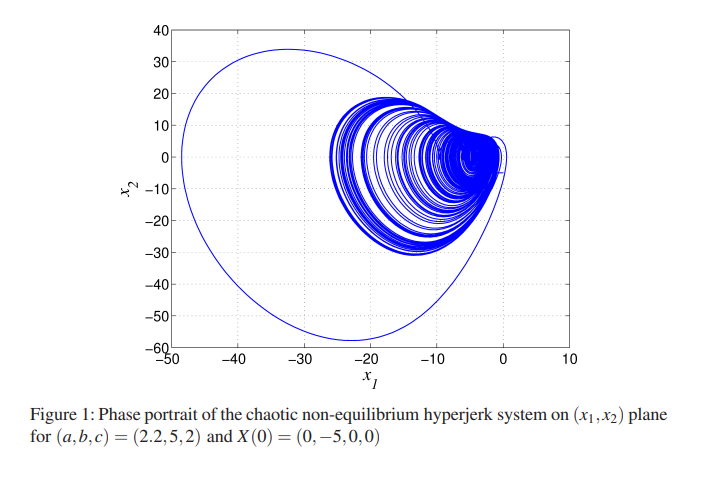
A 4-D chaotic hyperjerk system with a hidden attractor, adaptive backstepping control and circuit design
A novel 4-D chaotic hyperjerk system with four quadratic nonlinearities is presented in this work. It is interesting that the hyperjerk system has no equilibrium. A chaotic attractor is said to be a hidden attractor when its basin of attraction has no intersection with small neighborhoods of equilibrium points of the system. Thus, our new non-equilibrium hyperjerk system possesses a hidden attractor. Chaos in the system has been observed in phase portraits and verified by positive Lyapunov exponents. Adaptive backstepping controller is designed for the global chaos control of the non
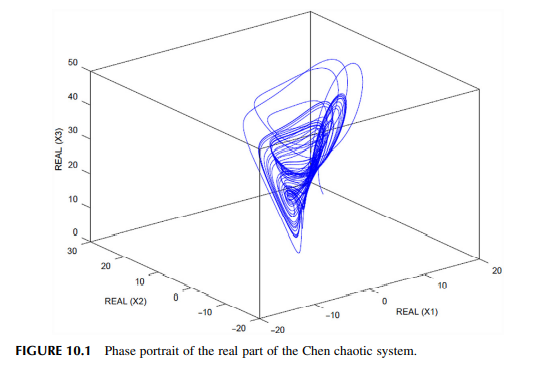
Sliding mode stabilization and synchronization of fractional order complex chaotic and hyperchaotic systems
This chapter is intended to design and analyze several sliding mode techniques for the stabilization and synchronization of fractional order complex chaotic and hyperchaotic systems. Considering that chaos is a hot topic nowadays due to the vast number of real physical systems such as mechanical, electrical, and chemical systems in which this phenomenon is found; this book chapter will provide novel sliding mode approaches for the stabilization and synchronization of chaotic and hyperchaotic systems. Fractional order chaotic and hyperchaotic systems have been proved to be difficult to

Image encryption in the fractional-order domain
This paper presents a new image encryption scheme based on the fractional-order Lorenz system which gives more degrees of freedom in key generation. In the modified fractional-order system, the key length is doubled using the three fractional-orde r parameters beside the three initial conditions, which makes it invulnerable to brute-force attacks. In addition, using a very simple algorithm, based on pixel confusion only, strongly encrypted images are produced. Such an algorithm can be used in real time applications. To evaluate the algorithm and analyze the encryption results, a standard image
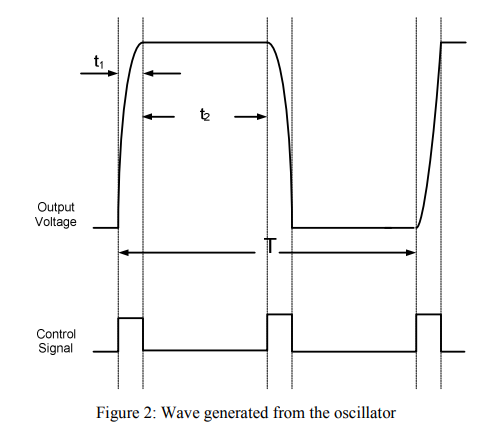
Design methodology for square wave resonant clock generators
Resonant clocking is a promising low power alternative for conventional clocking method. In this work, a design methodology is presented for square wave resonant clocking technique to assure minimum power consumption. These equations were verified by designing a differential clock generator which showed 55% power savings compared to conventional clocking. © 2012 IEEE.
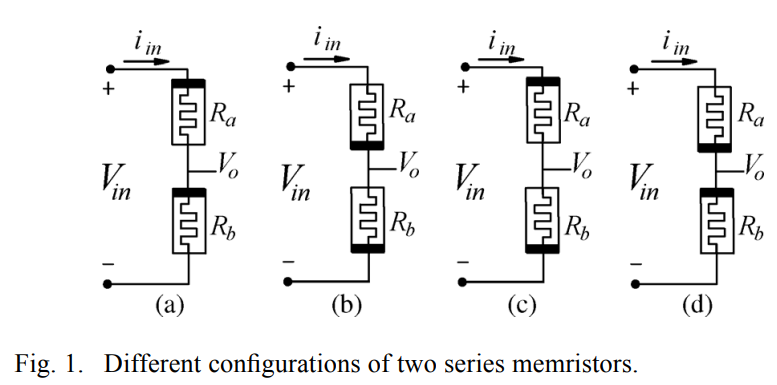
Generalized analysis of symmetric and asymmetric memristive two-gate relaxation oscillators
Memristive oscillators are a novel topic in nonlinear circuit theory, where the behavior of the reactive elements is emulated by the memristor. This paper presents symmetric and asymmetric memristive two-gate relaxation oscillators. First, the analysis of the two series memristors is introduced to study the effect of changing their polarities, as well as the mobility factor to be used in the two-gate relaxation oscillator instead of the RC circuit. The generalized analysis for the proposed memristive two-gate oscillator is introduced, where the generalized expressions for the oscillation
Pagination
- Previous page ‹‹
- Page 8
- Next page ››
