Numerical solution to a 2D-problem of piezo-thermoelasticity in a quarter-space within the dual-phase-lag model

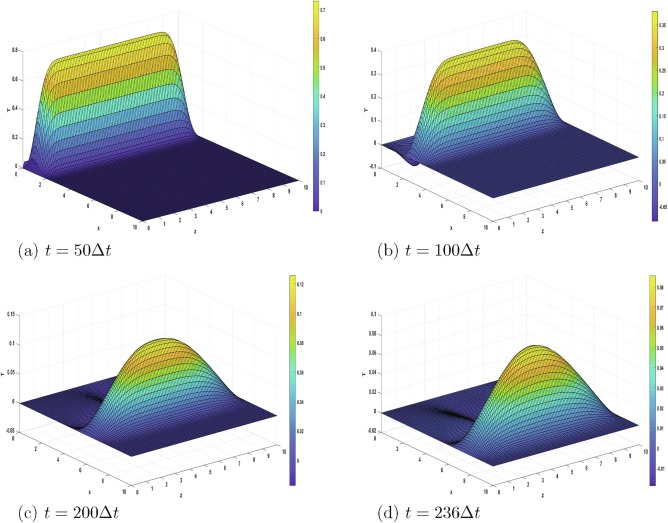
We present a numerical solution by finite differences to a linear, plane, initial-boundary-value problem of thermo-piezoelasticity in a quarter-space, within the dual-phase-lag model. Motion is excited by a one-period heat regime applied to one boundary of the medium. The relation between the two relaxation times is clarified in order to obtain wave-like solutions. An explicit, three-level numerical scheme is proposed to solve the problem under concrete initial and boundary conditions. The obtained results are discussed and three-dimensional plots of the unknown functions are presented. They clearly represent the traveling wave character of the solution in the initial stage. The effect of thermal relaxation is clearly observed in the given spatial distributions of heat, mechanical displacement, electric potential and electric field. In contrast to other methods which put severe restrictions on the geometry of the domain and on the type of boundary conditions, the present method allows to deal with rather general geometries and boundary conditions. The case of a non–homogeneous medium can be treated as well, thus providing the opportunity to solve various problems of practical importance. It is believed that the present results may be of interest in measuring the thermal relaxation times of materials, and that the study may find applications in various smart structures. © 2020 Elsevier B.V.