Computing the burrows-wheeler transform of a string and its reverse
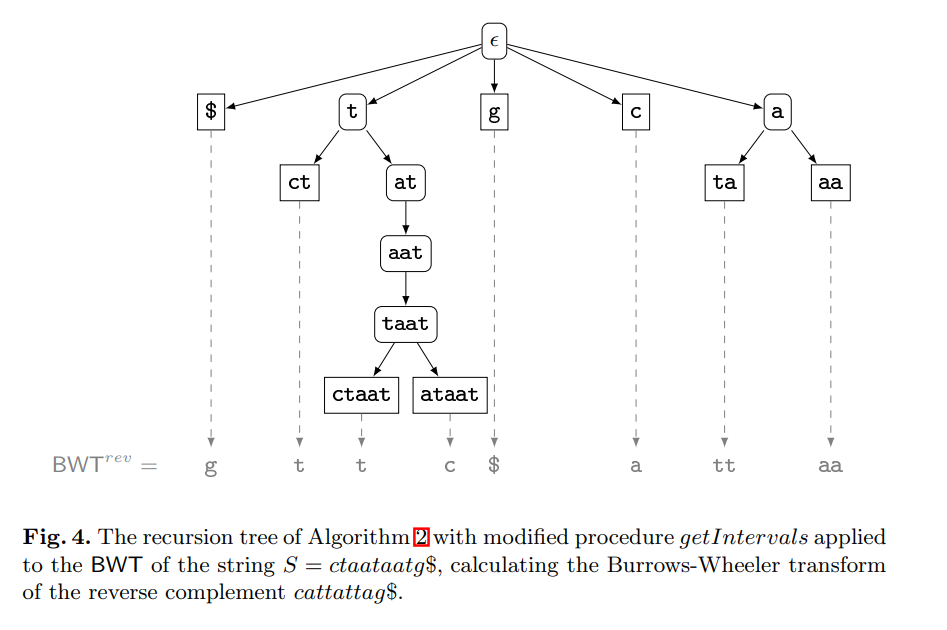
The contribution of this paper is twofold. First, we provide new theoretical insights into the relationship between a string and its reverse: If the Burrows-Wheeler transform (BWT) of a string has been computed by sorting its suffixes, then the BWT and the longest common prefix array of the reverse string can be derived from it without suffix sorting. Furthermore, we show that the longest common prefix arrays of a string and its reverse are permutations of each other. Second, we provide a parallel algorithm that, given the BWT of a string, computes the BWT of its reverse much faster than all known (parallel) suffix sorting algorithms. Some bioinformatics applications will benefit from this. © 2012 Springer-Verlag.